改訂増補版:統計検定を理解せずに使っている人のためにII
katosei.jsbba.or.jp/view_html.php?aid=1196
改訂増補版:統計検定を理解せずに使っている人のためにII
改訂増補にあたって この総説は,「統計検定を理解せずに使っている人のためにII」の改訂増補版であり,「改訂増補版:統計検定を理解せずに使っている人のためにI」の続きである.改訂
katosei.jsbba.or.jp
---------------------
Kagaku to Seibutsu 57 (9) : 562-579 (2019)
세미나 실
개정 증보판 : 통계 검정을 이해하지 않고 사용하는 사람들을 위해 II
이케다 郁男
토호쿠 대학 미래 과학 기술 공동 연구 센터
Published : 2019-09-01
© 2019 公益社 사단 법인 일본 농예 화 학회
개정 증보있어서
이 총설은 "통계 검정을 이해하지 않고 사용하는 사람들을 위해 II」의 개정 증보판이며,"개정 증보판 : 통계 검정을 이해하지 않고 사용하는 사람을 위해 I '의 자세히이다. 개정 증보있어서의 자세한 내용은 "개정 증보판 : I '의 시작 부분을 읽어 주셨으면한다. 이 개정 증보판에서는 "II"에 있던 오류를 수정했다. 또한 이해하기 어려운 부분에 대해 더 알기 쉽게 설명하기 위해 노력했다.
"개정 증보판 : I '는 모집단 , 표본 , 어머니 분산 , 모 표준 편차 , 표본 분산 , 표본 표준 편차 , 공정한 분배 , 불편 표준 편차 , 파라 메트릭 검정과 비모수 검정의 차이 , 정규성 검정 에 대해 주로 에 기술했다. 이러한 이해가 애매한 경우는 다시 "개정 증보판 : I '를 읽고 싶다. 이번에는 표준 오차 , 2 군의 파라 메트릭 테스트의 기본 , 상당한 차이의 의미 , 2 군의 비모수 검정의 기본 을 주로 서술했다. 또한,도 번호는 지난번 '개정 증보판 : I'에서의 일련 번호이다. 먼저 그림의 내용을 대충 바라보다가 글을 읽어주기 바란다.
파라 메트릭 검정 (그림 16)

그림 16 ■ 파라 메트릭 테스트
파라 메트릭 검정은 모집단이 정규 분포되어 있다고 가정한다 ( 그림 16 ). 평균과 분산 등의 매개 변수를 사용에서이 명칭이있다. 파라 메트릭 시험의 예로는 Student의 t 검정과 분산 분석 등이있다. 이전과 마찬가지로 모집단의 크기는 N , 어머니 평균 μ 어머니 분산 σ 2 로 정의한다. 모평균 μ 어머니 분산 σ 2 인 정규 분포를 N (μ, σ 2 )으로 설명하기로한다.
파라 메트릭 테스트의 기본 : 모집단에서 추출 된 n 개의 표본 평균 (표본 평균)의 분포를 생각한다 (그림 17)

그림 17 ■ 파라 메트릭 테스트의 기본
꽤 붐비 어 들어간 이야기가되므로주의 해 읽으면 좋겠다. 차분히 읽지 않으면 어렵지만, 여기를 이해할 수없는 경우 표준 오차 SE 및 t 검정은 이해할 수 없다. 여기에서는 모집단에서 추출 된 n 개의 표본 평균 (표본 평균) X ̄ i 의 분포를 생각한다. 개별 표본 데이터의 분포가 아닌 것에주의하기 바란다.
그림 17 에서와 같이 정규 분포하고있는 모집단 N (μ, σ 2 )에서 n 개의 표본을 추출 표본 평균 X ̄ 1 을 계산한다. 이것을 여러 번 반복하면 각각 표본 평균 X ̄ 1 , X ̄ 2 , X ̄ 3 ...이 얻어진다. 이 많이 얻은 표본 평균을 하나의 다른 모집단 생각 분포를 살펴보면 정규 분포하여 그 평균값은 모평균 μ에 접근 하는 것으로 알려져있다 * 1 아래 그래프). 또한, n 이 큰 경우 모집단이 정규 분포뿐만 아니라 정규 분포에서 벗어나 있어도 그 모집단에서 채취 한 표본 평균의 분포는 정규 분포한다는 재미있는 성질이있다. . 그러나 첫 번째 모집단의 정규 분포 N (μ, σ 2 )과 편차 방법 (모집단 분산) σ 2 가 달리 1 / n 만큼 작은 편차 방법 σ 2 / n될 수 이미 알고있다. 즉, N (μ, σ 2 / n )의 정규 분포가된다 ( 그림 17 아래 그래프) * 1 . 즉, 표본 평균의 어머니 표준 편차 n 은σ2/ n----√= σ/n--√ 되어, σ보다 1 /n--√뿐만 작아진다 * 2 . 그림 17 에서는 예로서 어느 하나의 표본 평균 X ̄ 1 의 위치를 정규 분포 그래프에 빨간색으로 보여주고있다.
정규 분포를 표준 정규 분포로 변환한다 (그림 18)

그림 18 ■ 표준 정규 분포로 데이터 변환
정규 분포는 μ와 σ 2 가 다르면 분포가 다르기 때문에 ( 그림 18 왼쪽과 왼쪽의 그래프와 같이) 다양한 모집단에서 일일이 다른 정규 분포를 사용하여 생각하는 것은 귀찮은이다. 그래서 모평균 μ가 0 (제로)에서 σ 2 1 2 정규 분포를 표준 정규 분포 로 정의하고 각각의 다른 정규 분포를 표준 정규 분포로 변환 하는 생각으로 정해져있다. 그러면 어떤 μ와 σ 2 의 모집단에서도 표준 정규 분포에서 생각할 수있다. 그림 18 의 오른쪽의 그래프가 표준 정규 분포이다 * 3 . 방금 전의 표본 평균 X ̄ 1 ( 그림 17 아래 그래프와 그림 18 왼쪽과 왼쪽 그래프)를 표준 정규 분포의 값으로 변환하는 것으로한다 (이를 표준화 라고 부른다). 첫째, 표준 정규 분포에서 모평균은 제로이기 때문에 모평균 μ를 제로로 이동하기 위해서는, μ로 당겨 주면된다. 즉, ( X ̄ 1 -μ)이다. 한편, 표준 정규 분포에서 모집단 표준 편차는 1이기 때문에,σ/n--√를 1로 변환하기 위해서는σ/n--√로 나누어 주면된다. 즉, 표본 평균 X ̄ 1 을 표준화하고 변환 한 값을 Z 1 하면 다음의 식으로 나타낼 수있다 ( 그림 18 중앙 식).
Z1=(X¯¯¯1- μ )σn√
그러면 X ̄ 1 은 그림 18 오른쪽 표준 정규 분포 그래프 중의 Z 1 로 변환되는 * 4 . 이러한 표준화를 실시하면 다른 모집단의 정규 분포 ( 그림 18 의 왼쪽과 아래 그래프) 표본 평균에서도 마찬가지로 표준 정규 분포 데이터 변환 할 수있다.
이 데이터 변환은 매우 중요하다 조금 이해하기 어렵다. 그래서 수식에서는 이해하기 어렵 기 때문에 간단한 예를 나타낸다. 그림 19 을 보았 으면 좋겠다. 지금 제 1의 모집단으로 μ = 10, σ/n--√= 2 인 정규 분포가 있고 X ̄ 1 = 12 표본 평균을 얻을 수 있었다고한다 ( 그림 19 왼쪽 그래프). 다음으로, 제 2의 모집단으로 μ = 20,σ/n--√= 4의 정규 분포가 있고 X ̄ 1 = 24가 얻을 수 있었다고한다 ( 그림 19 왼쪽 그래프). 이러한 숫자를 위 식에 대입하면 모두 Z 1 = 1을 얻을 수있다 ( 그림 19 중앙 식 오른쪽 그래프). 이러한 2 가지 정규 분포에서 모평균 μ 어머니 표준 편차σ/n--√표본 평균 X ̄ 1 의 수치는 각각 다르지만, 표준 정규 분포 데이터 변환하면 같은 값이 표준 정규 분포의 Z 1 의 위치는 두 모집단에서 동일한 지 알 수있다. 표본 평균 X ̄ 1 이 표준 정규 분포중인 Z 1 에 표준화 된 것을 알아두기 바란다.

그림 19 ■ 표준 정규 분포의 표준화 사례
모집단 표준 편차 σ는 모르기 때문에 불편 표준 편차 u로 대체 (그림 20)
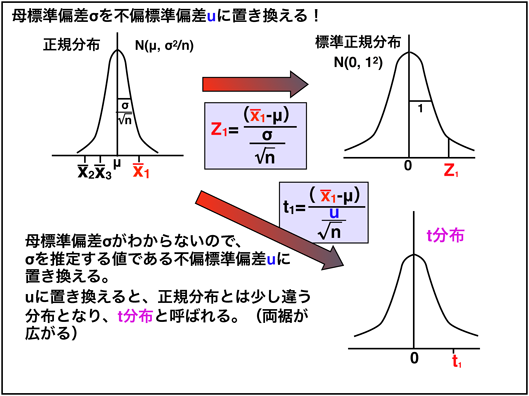
그림 20 ■ 모집단 표준 편차 σ의 불편 표준 편차 u로 대체
지금까지 정규 분포하고있는 모집단에서 추출 된 표본 데이터의 평균 즉 표본 평균의 분포는 정규 분포하는 언급했지만 ( 그림 20 왼쪽 그래프이를 N (μ, σ 2 / n ) 한), 편차 (모집단 표준 편차)은σ/n--√이다. 여기에 원래의 모집단 모집단 표준 편차 σ는 생명 과학 연구는 일반적으로 알 수없는 값이며,이 상태로는σ/n--√를 계산할 수 없다. 그러면 우리는 어떻게해야 하는가?
여기서 마지막 "개정 증보판 : I '에 등장한 불편 표준 편차 u 기억했으면 좋겠다 (이전의 그림 12 및 13) * 5 . 표본 데이터에서 모집단 표준 편차 σ를 추정하는 값으로 계산할 수있는 것이 불편 표준 편차 u이다. 그래서 어머니 표준 편차 σ를 불편 표준 편차 u를 대체한다. 이 계산 값을 t 1 로한다.
t1=(X¯¯¯1- μ )un√
그래서 몇번이나 표본을 가지고 표본 평균 X ̄ 1 , X ̄ 2 , X ̄ 3 ... 및 u 1 , u 2 , u 3 ...을 계산하고, t 1 , t 2 , t 3 ...을 계산てt 값의 분포를 조사한다. σ를 이용한 경우 분포는 정규 분포하기 때문에 표준 정규 분포로 변환되었지만 ( 그림 20 왼쪽 그래프에서 오른쪽 그래프에) u로 대체하면 정규 분포와는 조금 다른 분포된다 ( 그림 20 왼쪽 그래프 위에서 오른쪽 아래 그래프에) * 6 의 그래프 참조). . 이 분포는 t 분포 라고 명명 된 ( 그림 20 오른쪽 그래프와 그림 21 의 그래프). t 분포의 그래프는 정규 분포보다 양 밑단이 확산되고있는 것에주의 해 주었으면한다.

그림 21 ■ 표준 정규 분포와 t 분포의 차이
불편 표준 편차 u는 모집단 표준 편차 σ를 추정하고있다. 그러나 u는 참 불편 표준 편차가 아니기 때문에 표본의 크기 n 의 영향을받는 * 6 의 그래프 참조). . n 이 작고 큰 영향을받지 u는 σ에서의 차이가 크고, 값은 작아진다 (개정 증보판 : I의 * 13 참조). 한편, n 을 크게 취하면, u는 그다지 영향을받지 않고 σ에 가까운 값이된다 * 5 . t 1 식 및 그림 21 의 t 분포 그래프를보고 싶어하지만, n 이 작은 u는 σ보다 작은 값이되기 때문에 계산 된 t 값은 t 분포의 중심의 제로로부터 떨어진 값이되는 경우 이 상대적으로 많아진다. 그렇다면, 정규 분포에 비해 t 분포의 저변이 상대적으로 확산된다. 한편, n 이 커지면 u는 σ에 접근하기 때문에, t 값의 분포는 정규 분포에 가까워지는 ( 그림 21 의 그래프). 즉, t 분포는 n이 다르면 그래프의 모양이 다르다는 것을 알아두기 바란다 * 7 .
여기에서는 표본 평균의 분포와 편차를 생각해 온에서 위의 t 1 식의 분모이다u /n--√표본 평균이 어떤 불균형 방법을하고 있는지를 보여주고 있으며, 이것은 많은 연구자들이 사용하는 표준 오차 ( standard error; SE )이다.σ/n--√표본 평균의 어머니 표준 편차 였으므로 ( 그림 17 ), 표준 오차는 표본 평균의 모집단 표준 편차를 추정하는 값이된다 . 즉, SE는 모평균 μ 가 어디 쯤에 있는지 , 즉 모평균 μ 의 가능한 범위 를 나타내고있다.
SE를 표본 데이터의 편차의 일종이라고 생각하는 독자가 있을지도 모르지만, 그것은 실수이며, SE에는 표본 데이터의 편차의 의미는 없다. t 1 식의 분모가 SE이기 때문에, 위의 식은 다음과 같이도 쓸 수있다.
t1=(X¯¯¯1- μ )SE
즉,이 수식은 모평균 μ의 가능한 범위 인 표준 오차 SE를 기준 (분모)로하여 표본 평균 X ̄ 1 이 모평균 μ에서 어느 정도 떨어져 있는지 (분자)을 계산하고있다 이다. 예를 들어, X ̄ 1 -μ> 0이라고 가정하여 분모의 SE가 작 으면 분자 ( X ̄ 1 -μ)는 상대적으로 커지므로 t 1 값은 처음부터 떠난다. 반대로, SE가 크면 ( X ̄ 1 -μ)는 상대적으로 작아 지므로 t 1 값은 제로에 가까워진다. 이 감각을 이해했으면 좋겠다.
표본 평균 ± SE는 무엇을 의미하고 있는지? (그림 22)

그림 22 ■ 표본 평균 ± SE의 의미
표본 데이터의 평균 (표본 평균)은 모평균 μ를 추정하는 값이라고 평가된다. 그리고 SE는 모평균 μ의 가능한 범위를 나타내고있다 ( 그림 22 ). SE 식을 보면 SE는 표본의 크기 n 이 커질수록, 작아지는 것을 알 수있다. 이것은 n 이 증가하면 증가할수록, 모평균 μ의 존재 범위가 좁혀진 것을 의미한다. n 이 증가하여 모집단의 크기 N 에 가까이할수록 μ가 좁혀지고가는 것은 감각적으로 이해할 수있는 것이 아닐까 * 8 .
표본 평균 ± SD 및 표본 평균 ± SE는 무엇이 다른가? (그림 23)

그림 23 ■ 표본 평균 ± SD 및 표본 평균 ± SE의 차이
표본 평균 ± SD 내용은 이전의 그림 15에서도 설명했듯이, 연구자들은 모평균 μ와 어머니 표준 편차 σ 모두에 관심이있는 것이다 ( 그림 23 ). 그러면, 표본 평균 ± SE는 어떻게 일까? SE는 모평균 μ의 가능한 범위를 나타내고 있기 때문에 모평균 μ에 관심이 집중되고있는 것이며, 어머니 표준 편차 σ는 원칙적으로는 관심이없는 것입니다. 모평균 μ를 SE 따라 어디까지 좁힌 여부가 초점이다 (이 점은 "편안 생물 통계학」( 2) 에 선발되어있다).
실례를 그림 23 중간에 보여주고있다. 있는 기능성 성분이 모평균 μ를 변화시키는 여부에만 관심이있는 경우, SE를 사용하면된다. 그림 23 하단에 나타내는 예에서는 SD가 적당하다. 그러나 학회 발표 나 논문을 보면 한, SE와 SD 위의 관점에서 구분하고있는 연구자는 적은 것 같습니다. SD를 사용하거나 SE를 사용하거나 실험실마다 정해져있는 것이 아니라 어디 까지나 무엇을 알고 싶은지에 달려 있는 것이다. 이 세미나의 독자는 SD 하느냐 SE하는 것인지 잘 생각해 구분하라.
2 군의 차이 검정 (Student의 t 검정) (그림 24, 25)

그림 24 ■ 통계 검정 중요한 포인트

그림 25 ■ 2 군의 표본 평균의 차이도 정규 분포하는!
여기에서 드디어 군간 비교 군간의 유의 한 차이 검정에 들어가 "상당한 차이"에 대해 설명 할 예정이다. 생명 과학의 연구에서는 2 군 또는 3 군 이상을 설정하여 군 간 비교 실험이 많은 것이 아닐까? 그 기본이되는 것이 Student의 t 검정이다. t 검정은 2 군의 파라 메트릭 테스트이며, t 분포를 이용하는 것으로부터 그 이름이있다. 그러나 통계 설명서를 읽어도 계산 방법은 알지만, 그 원리는 쉽게 이해할 수없는 경우가 많다. 꽤 복잡하다, t 검정의 원리를 마스터하면 다른 다양한 검정도 실은 기본적인 절차는 동일 이기 때문에 쉽게 이해할 수있을 것이다.
자세한 내용은 후술하지만, t 검정에 주로 대응이없는 독립 2 군의 검정 (unpaired t test)와 대응되는 관련 2 군의 검정 (paired t test)가있다. 여기에서는 unpaired t test를 예로 상술한다.
그림 24 의 오른쪽 그림은 2 군의 표본 평균 X ̄ 1 과 X ̄ 2 가 나타나고있다. 이 두 군 사이에 "차이가있다"여부가 기준이 없다고 결정할 수 없다. 예를 들어, X ̄ 1 과 X ̄ 2 사이에 10 % 이상 차이가 있으면 차이가 있음을 하자는 기준이다. 그러나 '개정 증보판 : I "의 그림 4에서 설명한 바와 같이 차이가 있는지 여부는 표본 평균의 차이뿐만 아니라 데이터의 편차 방법에 따라 판단이 달라질 때문에 기준을 결정하는 것은 곤란하다 . 그래서 통계는 "차이가 없다"는 가설에서 생각해가는 것이 정해져있다. 이 '차이가 없다'는 가설을 귀무 가설 이라고 부른다. 이에 대해 '차이가있다'는 가설을 대립 가설 이라고 부른다. "차이가 없다"에서 생각해 갈 생각은 군간 비교 시험에서는 기본적인 생각이며, 공통점 때문에 기억했으면 좋겠다.
그래서 생각으로 동일한 모집단에서 표본을 취할 생각 ( 그림 24 그림 참조). 예를 들어, 좀 더 모집단에서 각각 n 1 과 n 2 개의 표본을 가지고 2 군으로한다. 이 경우 두 군의 각각 개별 표본은 지원 (관련)이 아닌 독립하고 있기 때문에, 대응이없는 독립 2 군의 검정 (unpaired t test)이다. 2 군 각각의 표본 평균 X ̄ 1 과 X ̄ 2 로한다 ( 그림 24 ). 이러한 표본을 취하면 원래 같은 모집단이기 때문에, 본래는 차이는 없을 것이다하지만 표본이므로 표본 평균 X ̄ 1 과 X ̄ 2 는 반드시 일치하지 않는다는 상황이다.
여기에서 편의적으로 두 표본 X ̄ 1 과 X ̄ 2 모집단의 모평균을 각각 μ 1 과 μ 2 로 어머니 분산 σ 1 2 과 σ 2 2 로한다. (동일한 모집단에서 표본이기 때문에, 실제로 μ 1 = μ 2 및 σ 1 2 = σ 2 2 이다). 여기에서 귀무 가설은 "차이가 없다"고하기 때문에 μ 1 = μ 2 가된다. 이에 대해 대립 가설은 "차이가있다"고하므로 μ 1 ≠ μ 2 가된다.
모집단에서 n 개의 표본을 가지고 표본 평균 X ̄ i 를 얻은로서이를 무한히 반복 할 때 표본 평균은 정규 분포 어머니 분산 σ 2 / n , 어머니 표준 편차는σ/n--√이된다는 것은 이미 언급 한 ( 그림 17 아래 그래프). 그러면 어떤 정규 분포 모집단에서 표본 데이터를 n 1 과 n 2 개 꺼내 표본 평균 X ̄ 1 과 X ̄ 2 를 구한다. 그리고 표본 평균의 차이 ( X ̄ 1 - X ̄ 2 )를 요청할으로이 작업을 반복하여 ( X ̄ 1 - X ̄ 2 )의 분포를 구하면, 어떻게 될 것인가? 사실이 경우에도 정규 분포하기 때문이다 ( 그림 25 왼쪽 그래프). ( X ̄ 1 - X ̄ 2 )는 같은 모집단에서 표본 평균의 차이 때문에 0을 중심으로 흩어지는 것으로 예상된다. 즉, 정규 분포의 중심은 μ 1 -μ 2 = 0이다. (X ̄ 1 - X ̄ 2 )를 하나의 모집단 할 때의 모집단 분산은 각 군의 어머니 분산 σ 1 2 / n 1 및 σ 2 2 / n 2 를 더한 값이된다. 즉
σ12n1+σ22n2
이 루트하여 모집단 표준 편차를 계산할 수있다.
즉, 모집단 표준 편차는
σ12n1+σ22n2---------√
이되지만, 원래 동일한 모집단이므로 σ 1 = σ 2 이기 때문에, 이들을 σ하면 다음식이되는 ( 그림 25 왼쪽 그래프).
σ1n1+1n2--------√
그래서 표본 평균의 차이 ( X ̄ 1 - X ̄ 2 )이 정규 분포의 어디에 있는지를 생각하지만, 여기서 그림 18 에서 설명한 표준 정규 분포에 대한 데이터 변환 ( 표준화 ) 을 기억했으면 좋겠다 .
( X ̄ 1 - X ̄ 2 )를 표준 정규 분포의 Z 1 로 변환하면 다음과 같은식이 출현 ( 그림 25 중앙에서 식).
Z1=X¯¯¯1-X¯¯¯2- (μ1-μ2)σ1n1+1n2------√
이 수식이 출현 할 와닿지 않는 것 같으면 " 정규 분포를 표준 정규 분포로 변환 ( 그림 18 ) "절을 다시 읽어 주었으면한다.
여기서 μ 1 -μ 2 = 0이기 때문에, 결국 다음의 식을 얻을 수 표준 정규 분포의 값으로 변환된다 ( 그림 25 오른쪽 그래프).
Z1=X¯¯¯1-X¯¯¯2σ1n1+1n2------√
여기서, σ는 원래의 모집단 모집단 표준 편차 이며, 연구자는 알 수 없다. 그래서 그림 20 에서 설명한 것과 같은 이유로, 모 표준 편차를 추정하는 값이다 공정한 표준 편차 u 를 사용하기로한다. 이 때의 계산 값을 t 1 하면 다음식이된다 ( 그림 25 하단 중앙 식).
t1=X¯¯¯1-X¯¯¯2u1n1+1n2------√
그런데, 여기에서 불편 표준 편차 u는 어떻게 계산하는 것일까? 불편 표준 편차 u의 계산 방법은 이전의 그림 12에서도 설명했지만, 여기에서는 그림 26 에서 식을 보았 으면 좋겠다. 간단하게는 제곱을 자유 n -1 나눗셈 해 공정한 분배를 요구 루트했다. 그러나 여기에서는 2 군 있기 때문에 2 군 모두의 편차를 고려해야한다. 그래서 2 군의 제곱을 합산하여 합산 한 자유도 나눗셈하여 루트하면된다 ( 그림 26 밑바닥 식).

그림 26 ■ ( X ̄ 1 - X ̄ 2 )의 공정한 표준 편차 u 계산
모집단에서 n 개의 표본을 가지고 표본 평균 X ̄ i 를 얻은로서이를 무한히 반복 할 때 표본 평균의 분포는 공정한 표준 편차 u를 이용하면 t 분포하는 것은 이미 언급 한 ( 그림 20 오른쪽 그래프). 이것과 마찬가지로, 위의 식으로 계산 한 t 1 이 계산을 무한 반복 t 분포하기 때문에 t 분포에서 값으로 변환된다 ( 그림 25 오른쪽 그래프). t 분포에 대해서는 그림 21 의 설명에서 자세히 설명했다.
이 t 1 값이 t 분포의 어디에 위치하는지에 상당한 차이를 결정 해가는 것이되는 것이다. 여기까지의 내용을 제대로 이해 한 후, 앞서 좋겠다.
여기까지 두 표본 평균의 차이 ( X ̄ 1 - X ̄ 2 )의 분포는 공정한 표준 편차 u 를 이용하면 t 분포하는 것을 말해왔다. 그리고 두 군의 실험을 실시하여 얻어진 데이터에서 t 1 을 계산했다. 이 t 1 을 t 분포의 어느 위치에 있는지를 조사한다 ( 그림 25 오른쪽 그래프 t 1 의 위치를 결정). t 분포 0을 중심으로 좌우에 바라つい있다. X ̄ 1 과 X ̄ 2 에 큰 차이가 없으면 ( X ̄ 1 - X ̄ 2 )는 제로 기준에 있지만, 우연히 큰 차이가 있으면 처음부터 떠난다. 그러나 t 분포의 그래프에서 알 수 있듯이 처음부터 크게 떠날 확률은 낮아 좀처럼 일어나지 않는다. 그래서t 1 을 t 분포 한참 벗어난 근처에 오면 그것은 자주 발생하지 않는다 드문 일이 일어난 것이기 때문에 차이가 있음을 버리자는 것이 " 큰 차이가있다 "라고 결정 방법 에 되고있다. 즉, 같은 모집단에서의 두 표본 평균의 차이 ( X ̄ 1 - X ̄ 2 )를 "차이가 없다"는 귀무 가설 μ 1 = μ 2 에서 생각해 왔지만, "차이가 없다"고 생각에 너무 벗어난 근처에 있으므로 귀무 가설 μ 1 = μ 2 를 버리고 (기각) 차이가 μ 1 ≠ μ 2 는 생각을하게 해 버리려는 생각이다 (대립 가설 를 채택하기로한다). 이 "차이가 없다"에서 생각해 왔지만, 너무 차이가 크기 때문에 '차이가있다'로 버리려는 것이 군 간의 비교 검정의 기본 개념 이기 때문에, 기억하고 원한다.
여기서 중요한 포인트가 보인다. 즉, 두 군간에 "상당한 차이가있다"는 "진정한 차이가있다 '는 것을 의미하는 것은 아니다 이다. 많은 연구자는 표본으로 연구하고있다. 표본에서 연구하고있는 한, 비록 상당한 차이가 있어도 차이가 있다고 단정 할 수 없기 때문이다. 따라서 표본을 이용한 1 회 시험만으로는 진실 여부는 알 수 없다. 연구자들은 다양한 각도에서 연구하고 진실을 추구해야한다.
또한, t 분포는 자유도 n -1에 의해 분포의 형태가 변화하는 것은 이미 말했다 ( 그림 21 과 * 7 ). 여기에서는 2 군 있기 때문에 자유도는 그림 26 에서 언급 한 바와 같이 합산하여 ( n 1 -1) + ( n 2 -1)되고, n 1 + n 2 -2이다. 따라서 자유도 n 1 + n 2 -2 t 분포로 생각된다.
자주 발생하지 않는다 드문 확률의 결정 방법 (그림 27)

그림 27 ■ 유의 수준 (위험 요소)이란?
그럼 거의 일어나지 않는 드문 확률을 어느 정도 취하면 좋은 것이 있을까? 그림 27 위에 쓴대로, t 분포 전체 면적의 양단 각각 2.5 % 또는 0.5 %의 총 (또는 한쪽 이에 대해서는 후술한다)의 5 % 또는 1 %로하기로 정해져있다 (모집단을 1면, 0.05 또는 0.01) * 9 . 이 판정 기준을 유의 수준 이라고 부른다. 표본 평균 X ̄ 1 과 X ̄ 2 는 어느 쪽이 큰 값되는지 모르는 경우는 ( X ̄ 1 - X ̄ 2 )은 플러스가 될지 마이너스가 될지 모르기 때문에 t 분포 좌우 양단이 설정되어 각각 2.5 % 씩 또는 0.5 % 씩 t 값이 들어 오면 드문 일이 있다고 판정하는 것이다. 그러나 자주 발생하지 않는다 드문 일이라고해도 원래 "차이가 없다"에서 생각해 온 것이며, "차이가있다"고 단언하는 것은 위험하다. 그래서 유의 수준은 위험 요소 라고도 불린다. 또한 귀무 가설은 올바른, 즉 차이가 없는데 귀무 가설을 기각하는, 즉 차이가 있다고 해 버리는 오류를 범하는 것은있을 수있다. 이 오류를 제일 종의 과오 라고 부른다 * 10.
최근에는 t 값을 알면 PC에서 t 값보다 양쪽의 면적을 계산 해준다. t 분포의 면적을 1로했을 때의 양단의 면적을 p 값이라고 부른다 ( 그림 28 ). 따라서 유의 수준 (위험 요소)은 p 값이 0.05 (5 %) 또는 0.01 (1 %)이다. p 는 probability의 머리 글자이며, p 값은 관찰 된 차이가 우연히 생길 가능성을 나타내는 척도 라는 것이다. 예를 들어, p = 0.005는 관찰 된 차이가 우연히 일어나는 것은 0.5 %, 즉 200 번에 1 번임을 나타낸다. 우연히 일어나는 것이 200 번에 1 번이면 우연히 일어난 것이 아니라, 어떤 의미를 가지고 (크게) 일 가능성이 높다고 판단한다. 이것을 " 큰 차이가있다 "고 표현한다.
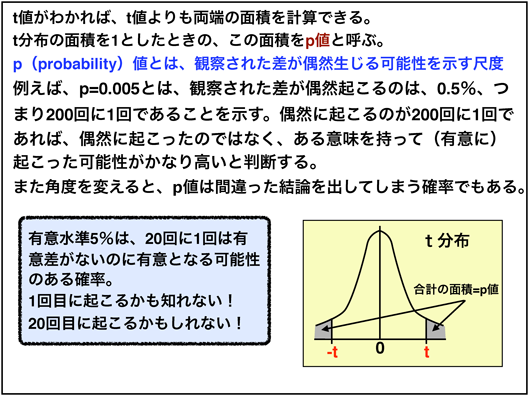
그림 28 ■ p 값은?
유의 수준 5 %에서 생각하면 ( 그림 28 왼쪽 프레임에서) 유의 수준 5 %는 같은 실험을 20 회 실시하면 1 회 정도는 큰 차이가 없는데 의미가 될 수있는 확률이다. 그것은 첫 번째 일어날지도 모른다! 20 번째로 생길지도 모른다! 실험은 일반적으로 1 회 밖에 실시하지 않는다. 만약 1 차에 일어나면, 사실은 큰 차이가 없는데 유의 한 차이가 있다고 판정된다 (첫 번째 종류의 과실). 연구팀은이 점을 염두에두고 두어야한다. 1 회 실험만으로 결과를 논문 화하는 위험성은 여기에서있다 . 이것은 아까 언급했듯이, 진실을 밝히기 위해서는 각도를 바꾼 연구를 확인하는 것이 중요하다.
t 1 의 계산식의 분모 식을 보면,
u1n1+1n2--------√
n이 커질수록이 값이 작아지고, X ̄ 1 > X ̄ 2 가정하면 t 1 값은 커지는 것을 알 수있다. t 값이 커지면 t 분포의 가장자리쪽에 들리는 때문에 의미가 될 가능성이 높아진다. 따라서 t 검정은 표본 데이터의 크기 n 을 늘리면 큰 차이가 나타나기 쉽다. 미묘한 차이 밖에 없거나, 편차가 큰 것을 처음부터 알고있는 매개 변수의 경우 n 을 늘릴 유용한 수단이다.
p <0.05를 어떻게 표현 하는가?
상당한 차이를 어떻게 표현하는지는 그림 29 에 기재 한 바와 같다. 상당한 차이가있는 경우 "차이가 있었다!"라고 표현하는 것이 많지만, 지금까지 말해 온 것처럼, '차이가있다'는 표현은 적절하지 않다. 정확하게는 "유의 수준 5 % 미만으로 통계적으로 유의 한 차이가있다"가 맞다. 적어도 "(통계적으로) 상당한 차이가있다"라는 표현을 사용하게하고 싶다. 또한 p > 0.05의 경우는 "(통계적으로) 큰 차이가 없다"합리적인 표현이다.

그림 29 ■ p <0.05의 표현은?
모집단의 정보를 알고있는 경우 검정에서 통계적으로 유의 한 차이의 의미를 다시 이해!
독자는 통계적으로 유의 한 차이의 의미를 이해할 수있는 것일까? 상당히 복잡한 내용 이었기 때문에 다른 하나 핀과 오지 않을지도 모른다. 그래서 여기에서는 생명 과학 연구자가 사용하는 일은 거의 없다 모집단의 정보 (모평균 μ와 어머니 분산 σ 2 )를 알고있는 경우의 검정에 대해 설명하고 큰 차이 검정의 이해를 높이고 싶다. 이미 상당한 차이의 의미를 이해 한 독자는 아마 쉽게 이해할 수있을 것이다.
필자가 만든 가상의 모집단이지만, 일본인 남성의 신장의 분포를 정규 분포 모집단 생각 신장의 평균 (모평균)가 μ = 170 cm에서 모집단 표준 편차 σ = 10이다 것을 알고 있다고 가정하고 생각 ( 그림 30 위) (일반 생명 과학 계열 연구에서는이 부분을 알 수 그것을 알고 싶지만 위해 연구하고있다). 일본인 남성은 6,000 만명으로한다. 분포는 정규 분포이기 때문에 170 cm 전후의 사람이 많은 키가 상당히 높은과 낮은 사람의 수는 줄어든다는 종 모양이다 ( 그림 30 왼쪽 그래프). 여기서 170 cm 전후의 사람은 많이 있기 때문에 "일본인 남성과 동등하다고 판단한다." 한편, 신장이 정규 분포의 양쪽 한참 벗어난 근처에 있으면 170 cm에서 상당히 벗어나 있으며, 이러한 신장의 일본인은 좀처럼 없기 때문에, "일본인과 동등하다고는 말할 수 없다"고 판단한다. 이것이 큰 차이가 없거나,있는 것을 의미하는 통계 검정의 원리이다.

그림 30 ■ 모집단의 정보를 알고있는 경우 통계 검정의 개념 (1)
지금까지 통계 검정은 원래 차이가없는 곳에서 생각한다. 그러나 차이가 없다고하기에는 너무 차이가 크기 때문에 차이가 있음을 버리자 생각이라고 설명했습니다. 여기에서도이 개념은 동일하다. 원래 일본인이다. 그러나 일본인과 생각에 너무 키가 큰 (낮은) 때문에 일본인이라고는 할 수없는 것에 버리자 라는 생각이다.
여기에서 일본인과 동등하거나 동등하지만 여부를 판단하기위한 경계선으로 간주 한 것이 유의 수준 5 % 또는 1 % 이다. 6,000 만명의 5 %는 300 만명이다. 양쪽 각각 2.5 %는 150 만 명에 해당한다. 꽤 키가 큰 (낮은) 사람으로,이 양단 150 만명에 들어가 있으면 너무 키가 큰 (낮은) 때문에 일본인과 동등의 신장은하지 않기로 버리려고 생각한다. 이 통계 검정에서 "상당한 차이가있다"는 것을 의미한다.
또한 실례를 들면, 지금 여기에 신장 x 1 = 194 cm의 A 군이있다. A 군이 일본인과 동등의 신장 여부를 조사하고 싶은 (A 군은 일본인 여부가 확실치한다). 이를 위해 194 cm이 정규 분포의 어디 쯤에 있는지를 검사한다. 그림 30 왼쪽의 정규 분포에서 194 cm가 어디 쯤에 있는지를 조사 할 수도 있지만, 도 18 에서 설명한 것과 마찬가지로, μ = 0, σ = 1의 표준 정규 분포 에 적용하여 데이터를 표준화 하게 정해져있다 ( 그림 30 오른쪽 아래). 평균치를 제로 좌표 이동하는 모평균 μ를 당기고 σ를 1로하기 위해, σ 나눗셈한다. 그러면 다음 식 수 ( 그림 30 오른쪽 중앙 식).
Z1=(x1- μ )σ
μ = 170 cm, σ = 10이기 때문에,
Z1=( 194 - 170 )10= 2 . 4
가된다.
표준 정규 분포에서 양쪽 2.5 %에 해당하는 Z 값은 1.96 (또는 -1.96)로 정해져있다. 계산 값 2.4는 1.96보다 더 제로보다 먼 위치에 있습니다 ( 그림 30 오른쪽 그래프), 신장 194 cm의 A 군은 한참 벗어난 신장임을 알 수있다. 따라서 A 군은 일본인의 신장은 상당히 벗어나 있으므로, 일본인과 동등의 신장이라고는 할 수 없다고 판단한다 ( 그림 30 왼쪽). 여기에서 "A 군의 신장은 일본인과 동등하다"는 귀무 가설 되고, "A 군의 신장은 일본인과 동등하다고는 말할 수 없다"는 대립 가설 이다. A 군의 경우 귀무 가설을 버리고 대립 가설을 채택한다. 이것이 상당한 차이 검정이다.
따라서, A 군은 일본인으로는 너무 신장이 높기 때문에, 일본인과 동등의 신장은하지 않기로 버리려고 생각한 것이지, 결코 일본인과 동등이 아니라고 단정 한 셈 이 아니다. 일본인에서도이 키의 사람이 존재한다. 사실 A 군이 일본인 인 것은있을 수있다. A 군이 일본인이 없다고는 결코 단정 할 수 없기 때문이다.
A 군의 경우 표본으로 n = 1 이었지만 표본이 둘 이상인 경우에는 어떻게되는 것일까? 예를 들어, 일본 전체 대학생의 평균 신장이 μ = 170 cm에서 모집단 표준 편차 σ = 10 인 것을 알고 있다고 가정 (모집단) ( 그림 31 ). Y 대학의 무작위 추출한 학생 n = 25의 평균 신장은 X ̄ 2 = 174 cm였다. Y 대학의 학생들의 신장은 전국 평균보다 크다고 할 수 있다는 우려가 있었다고한다. 여기에서 귀무 가설은 전국 평균과 동등하다. 대립 가설은 전국 평균과 동등하다고는 말할 수 없다고 설정한다.

그림 31 ■ 모집단의 정보를 알고있는 경우 통계 검정의 생각 (2)
여기에서는 n = 25 표본 평균 174 cm가 초점이다. 이것은 일본인 학생의 모집단에서 25 명을 표본으로 취한 평균 (표본 평균)이다. 그러면 25 명의 표본을 가지고가는 것을 반복하여 얻은 표본 평균의 분포 에서 생각할 필요가있다. 이것은 그림 17 의 구성과 동일하므로 기억하라. 표본 평균의 분포는 정규 분포하고 모평균 μ를 중심으로 흩어지는. 그 편차 (모집단 표준 편차)은
σn--√
였다 ( 그림 17 및 31 중앙 그래프). 이 정규 분포에서 X ̄ 2 = 174 cm가 어디에 있는지를 생각하지만, 여러 번 논의했듯이, 여기에서도 표준 정규 분포를 표준화 ( 그림 18 및 31 식). 그러면 변환식은 다음이다. 얻어진 값을 Z 2 하면
Z2=X¯¯¯2- μσn√=174 - 1701025√= 2
가된다. ( 그림 31 오른쪽 그래프).
그래서 Z 2 = 2가 표준 정규 분포의 어느 위치에 있는지를 조사한다. 아까 설명했듯이 양쪽 2.5 % 일 때의 Z 값은 1.96이기 때문에, 2는 1.96보다 약간 크기 때문에, Y 대학의 학생의 신장은 겨우 전국 평균과 동일하다고는 말하지 못하고, 상당히 키가 높다는 결론이된다. 통계학에서는 이러한 생각을하는 것을 다시 인식했으면 좋겠다.
여기서 만약 표본의 크기 n 이 25 명보다 작 으면 상기 식의 분모σn√이 커지기 때문에 Z 2 의 계산 값은 1.96보다 작아진다. 그러면 통계적으로 유의 한 차이가 없으며 Y 대학의 학생은 전국 평균과 동등하게 할 수있다라는 결과가된다. 즉, 표본의 크기 n 이 작아 진다고 결론이 달라진다. n 이 작을수록 정보의 정확성이 결여 오므로, 전국 평균과 동등하다고 말하지 않을 수 없게 올 것이다.
여기서 아까 A 군 n = 1의 예에 돌아 오지만, Z 의 변환식은 다음이었다.
Z1=(x1- μ )σ
한편, Y 대학의 학생 25 명의 예에서는
Z2=x2- μσn√
였다. 이 Z 2 식에 n = 1을 넣으면 Z 1 과 같은 식임을 알게된다. 즉, 도 31 의 중앙 그래프는 n = 1의 경우, 왼쪽 그래프와 일치한다.
여기에서는 모집단의 정보를 알고 있기 때문에, 표준 정규 분포 검정 을 실시한 것을 알아두기 바란다. 이미 언급 한 t 검정은 모집단 표준 편차 σ를 알 수 없기 때문에 어쩔 수없이 불편 표준 편차 u를 이용해야했고,이를 위해 t 분포가 등장했다 ( 그림 25 ). 차이점은이 부분 뿐이다.
대립 가설을 세우는 방법으로 검정 결과는 다른! (그림 32)

그림 32 ■ 대립 가설을 세우는 방법
지금까지 2 군의 실험에서 동일한 모집단에서 표본으로 2 군으로 하였다. 2 군 각각의 모평균은 편의적으로 μ 1 과 μ 2 한 (동일한 모집단이기 때문 μ 1 = μ 2 인). 귀무 가설로 모평균 μ 1 과 μ 2 는 차이가 없다, 즉 μ 1 = μ 2 했다. μ 1 과 μ 2 는 어느 쪽이 큰 값이 될지는 일반적 모르겠어요. 그래서 대립 가설은 μ 1 ≠ μ 2 (즉 μ 1 -μ 2 ≠ 0)로 하였다. 표본 평균 X ̄ 1 과 X ̄ 2 에서 생각하면, ( X ̄ 1 - X ̄ 2 )은 플러스 또는 마이너스 모르겠어요. 따라서 t분포의 양쪽의 2.5 % 씩의 범위에 들어가면 유의 수준 5 %에서 유의 한 차이가 있다고한다. 이러한 검정 양측 검정 라고 부른다 ( 그림 32 ). 미지의 기능성 성분의 영향을 조사하는 경우는 보통 X ̄ 1 과 X ̄ 2 는 어느 쪽이 더 커지거나 모르기 때문에 양측 검정으로해야한다. 그러나 미리 μ 1 과 μ 2 중 하나가 크다는 충분한 정보 가있는 경우, μ 1 > μ 2 또는 μ 1 <μ 2 과 대립 가설을 세우기도 가능하다. 구체적인 예를 그림 32 왼쪽 아래에 설명하고있다. 만약 μ 1 <μ 2 과 대립 가설을 세울 수 있다면, ( X ̄ 1 - X ̄ 2 )은 마이너스가 될 것을 처음부터 기대할 수 있기 때문에, 도 32 의 t분포 그래프의 음극 쪽만을 생각하면 좋기 때문에 마이너스 측에 5 %를 설정할 수있다. 이러한 검정 단측 라고 부른다. 그림 32 오른쪽 그림을 보면 알 수 있듯이, 단측에서 양측 검정보다 마이너스 측의 t 분포 면적이 2 배가되므로 유의하게 움 알 수있다.
단측 검정을 사용할 수있는 충분한 증거가있는 경우이다. 그림 32 에 단측의 일례를 보여 주었다. 그러나 일반적인 생명 과학 연구는 충분한 입증이 없기 때문에 연구를하고있는 경우가 많기 때문에, 생명 과학 연구에서 단측 검정을 이용하는 것은 거의 없다 . 게다가, 몇몇 시험 물질에서 1, 2 번 실험을 시도 양측 검정에서 유의 한 영향을 얻었다 고해서 나중에 조금 조건을 바꾼 실험에서 단측 검정을 이용하여 유의 한 차이를 유지할 수 있 한다고 판단은 허용되는 것은 아니다. 어디 까지나 μ 1 과 μ 2 중 하나가 크다는 충분한 정보 가있는 경우에 한정된다. 원저 논문에서 일반적으로 양측 검정 또는 단측 가지 설명은 없지만, 상식적으로는 양측 검정을 실시하고있는 것이다. 통계 소프트는 한쪽 또는 양쪽 여부를 확인하고 검정에 진행되는 경우가 많기 때문에 틀리지 않도록해야한다. 만약 확인하지 않고 앞으로 통계 소프트가 있다면 보통은 양측 검정이 실시된다.
2 군의 파라 메트릭 테스트의 흐름
그림 33 에 2 군의 파라 메트릭 시험의 흐름을 설명하고있다. 지금까지 말해 온 것은 지원되지 않는 독립 2 군의 검정 unpaired t test이며 ( 그림 33 왼쪽 위에서 아래의 흐름) 동일한 모집단에서 표본이므로 모집단 분산은 동일, 즉 σ 1 2 = σ 2 2 가정 한 (2 군의 차이 검정 (Student의 t 검정 절 참조)). 그러나 표본으로 2 군을 취하고 있기 때문에, 우연히 분산이 동일하다고는 할 수없는 경우도 일어날 수있다. 분산이 동일, 즉, 등등 분산 여부는 등 분산 성의 검정 을 실시, 등등 분산 판정되면 unpaired t test를 실시 등 분산 판정되지 않으면, Welch 검정 을 실시하는 것이 단골로 많은 통계 설명서에 그렇게 적혀있다 ( 그림 33 왼쪽 아래로 흐름). 그러나 Welch 검정 은 분산이 아닌 경우뿐만 아니라 분산이 있는지 모르는 경우 에도 정확한 검정을 할 수 있기 때문에 최근에는 권장되고있다. 한편, unpaired t test는 등분 산에서 이탈과 검정이 부정확가된다. 즉, Welch 검정을 사용한다면, 등등 분산 성의 검정을 할 필요가 없다. unpaired t test는 2 군의 검정 단골처럼 알려져 왔지만, t 검정을 사용하면 실제로 Welch 검정 이 실행되는 통계 소프트도 나타나고있다. 먼저 등 산성 검정 에 대해 설명한다.

그림 33 ■ 2 군의 파라 메트릭 테스트의 흐름
등 산성 검정 ( F 검정)의 원리 (그림 34)

그림 34 ■ 등 산성 검정
이미 언급했지만, unpaired t test는 동일한 모집단에서 2 군의 표본을 가지고 각각의 모집단 분산을 편의적으로 σ 1 2 과 σ 2 2 할 때 동일한 모집단이라면 당연히 σ 1 2 = σ 2 2 이기 때문에 2 군의 분산은 동일 (등분 산)으로 검정이있을 수있다. 그러나 실제로는 얻을 수있는 것은 표본 데이터이며, 어머니 분산 모르기 때문에 두 군의 불편 분산 u 1 2 와 u 2 2 생각하지 않을 수 없다. 표본 데이터이기 때문에, u 1 2 와 u 2 2 가 반드시 가까운 값이되는 것이 아니라 동 떨어져 버릴 수도있다. 그러면 unpaired t test는 잘 검정 할 수 없다. 그래서 u 1 2 와 u 2 2 가 동 떨어져 있는지를 검정하는 방법 등 산성 검정 이있다. 이 검정은 F 검정 이라고도 불린다.
그림 34 위의 그림에서와 같이 동일한 모집단에서 2 군을 꺼내어 각각의 불편 분산 u 1 2 와 u 2 2 를 계산한다. 등 분산이면, u 1 2 = u 2 2 를 보면된다, u 1 2 = u 2 2 이면, u 1 2 / u 2 2 는 1이된다 (이 값을 F 라한다). u 1 2 와 u 2 2 가 멀리 떨어진 값이라면, u 1 2 / u 2 2 1에서 벗어난 값이된다. 이것을 이용한다. 그래서 모집단에서 2 군 갔고, F 값을 계산하는 것을 반복하여 플롯하면 어떤 분포가 출현한다 ( 그림 34 오른쪽 그래프). 이것을 F 분포 라고 부른다 * 11. u 1 2 / u 2 2 분포이기 때문에 마이너스는있을 수 없다. F 는 1 전후가 될 가능성이 가장 높기 때문에 1을 정점으로하여 1에서 멀어 질수록 적어진다 분포된다. 그래서 F 가 1 당에 있다고 등등 분산과 생각 ( 그림 34 에서 F 1 정도) 1에서 크게 떨어진 경우 (그림에서 F 2 와 F 3 전후) 등 분산 생각에 너무 떨어져있어 무리가 있다고 판정한다. 판정 기준이지만, t 검정의 경우와 마찬가지로 생각한다. 즉 전체의 5 %를 기준으로 생각한다. u 1 2 와 u 2 2 어느 쪽이 큰 값이 될지는 모르기 때문에 F 값은 1보다 커지거나 작아지는 모르겠어요. 그래서 양쪽의 2.5 % 씩을 기준으로하고 거기에 F 값이 들어간 경우 등 분산은 말할 수 없다고 판정하는 것에 하자는 생각이다. 이것이 등 산성 검정 의 원리이다 * 12.
그러나 표본의 크기 n 이 작 으면 불편 분산이 크게 바라つい오는 우려가 있으므로, u 1 2 / u 2 2 도 크게 변동 등 분산 여부의 판단이 어려워진다. n 이 작은 경우 등 산성 검정은 분산이 있다고 판단되는 경우가 많다. 이것은 분산이 아니라고 판단하려면 차이가 너무 크기 때문에 분산이인지하고있는 것에 지나지 않는다. 등 분산 여부의 판단은 일반적으로 n = 30 이상 필요로된다. 이러한 점에서 표본의 크기 n 이 작은 경우 등 산성 검정은 안되다 이다.
그러면 n 이 작은 경우 등 분산 판정 되어도, unpaired t test를 실시하는 것은 위험 할지도 모른다. 생명 과학의 연구는 n 이 30보다 작은 실험이 많은 것이 아닐까? 이러한 경우 Welch 검정을 선택하는 것이 타당하다고 생각된다 (Welch 검정은 다음 절에서 설명한다). 물론, n 이 큰 경우에도 Welch 검정은 사용할 수 있으므로, 결국 표본의 크기 n 에 관계없이, 등등 분산 성의 검정은하지 않고 Welch 검정 을 실시하면 좋다. 또한,이 시험의 흐름은 비교적 최근 추천되어오고 있지만, 아직 널리 인정받은 것은 아니고, 등등 분산 성의 검정 → unpaired t test라는 생각으로 쓰여진 책이 대부분이다. 이 논의에 대해 인터넷에 정리하고있다 ( 3) . 검정을 이용하는 만의 연구자에게이 논쟁은 성가신 중 하나에 결정 될 곳이다. 필자가 조사한 한에서 등분 산 성 검정은하지 않고 Welch 검정에 좋은 것으로 생각된다. 이 생각에서 그림 33 을 수정 한 것이 그림 35 이다.

그림 35 ■ 수정 버전 : 2 군의 파라 메트릭 테스트의 흐름
통계 소프트는 등 분산 성의 검정 후에야 unpaired t test와 Welch 검정 모두의 검정 결과가 표시되는 것이있다. 양자의 검정 결과가 같으면 그 결과를 채용하면되므로 아무런 문제가 없다. 그러나 n 이 작은 경우, 만약 unpaired t test와 Welch 검정의 검정 결과가 다르다고 곤란하게된다. 등 분산 성의 검정이 안되다는 두 검정 결과를 채택해야할지 결정할 수 없다. 이런 경우는 Welch 검정의 검정 결과를 채용하고 좋다고 생각된다.
Welch 검정 사고 (그림 36)

그림 36 ■ Welch 검정의 생각
Welch 검정의 개념은 unpaired t test의 생각과 비슷하지만, 분산이 다를지도 모른다 2 군으로 생각하기 때문에 모집단 분산이 다른 두 모집단에서 각각 표본을 취하고 2 군 했다고 생각하는 편이 생각하기 쉽다 ( 그림 36 왼쪽 그림). 즉, 모평균 μ는 같지만 어머니 분산은 두 개의 서로 다른 모집단에서 표본 생각이다. 편의적으로 두 모평균은 μ 1 과 μ 2 하지만, μ 1 = μ 2 이다. 각각의 표본 평균 X ̄ 1 과 X ̄ 2 로 ( X ̄ 1 - X ̄ 2 )를 계산한다. 이것을 반복 분포를 살펴보면 unpaired t test의 경우와 마찬가지로 정규 분포 ( 그림 36 오른쪽 그래프) * 1 아래 그래프). 또한, n이 큰 경우 모집단이 정규 분포뿐만 아니라 정규 분포에서 벗어나 있어도 그 모집단에서 채취 한 표본 평균의 분포는 정규 분포한다는 재미있는 성질이있다. . 이 때, 어머니 분산 σ 1 2 및 σ 2 2 다르기 때문에 다음 식과 같이 별도로 더하면에 합산 어머니 분산을 구한다.
σ12n1+σ22n2
이 루트 값이 모집단 표준 편차가된다 ( 그림 36 오른쪽 그래프).
σ12n1+σ22n2---------√
그래서 unpaired t test의 경우와 마찬가지로, ( X ̄ 1 - X ̄ 2 )를 표준 정규 분포 값을 표준화 ( 그림 36 오른쪽 그래프에서 중앙 아래 그래프에).
그렇다면 다음의식이 출현 (표준화 방법은 그림 18 참조). 그러면 ( X ̄ 1 - X ̄ 2 )는 표준 정규 분포의 Z 1 로 변환된다 ( 그림 36 중앙 아래 그래프).
Z1=(X¯¯¯1-X¯¯¯2) - (μ1-μ2)σ12n1+σ22n2-------√
unpaired t test의 경우는 다음 식이었다 ( 그림 25 ). 분모의 표준 편차의 차이를 인식 해 주었으면한다.
Z1=(X¯¯¯1-X¯¯¯2) - (μ1-μ2)σ1n1+1n2------√
여기서 μ 1 = μ 2 이기 때문에 분자 (μ 1 -μ 2 )는 0이 끌 수있다. 또한 σ 1 2 및 σ 2 2 모르기 때문에 각 군의 불편 분산 u 1 2 와 u 2 2 를 사용하게된다.
unpaired t test는 그림 26 에서와 같이 합산의 불편 분산을 계산했다. 이것은 2 군이 각각 분산이 있다고 가정했기 때문에 합산했다. 그러나 Welch 검정에서는 두 군의 어머니 표준 편차가 다르기 때문에 각 군의 불편 분산 u 1 2 와 u 2 2 를 그대로 대입한다. 그러면 표준화 식의 분모는 다음 t 1 식이다.
t1=(X¯¯¯1-X¯¯¯2)u12n1+u22n2-------√
이 t 1 값이 t 분포의 어디에 있는지를 조사한다 ( 그림 36 왼쪽 그래프).
이와 같이, ( X ̄ 1 - X ̄ 2 )를 표준 정규 분포를 표준화하는데, 모 표준 편차를 모르기 때문에 불편 표준 편차로 대체하여 t 분포되고, t 1 값이 t 분포 어디에 있는지를 생각 하는 단계는 unpaired t test의 경우와 동일한 지 알 수있다.
그러나 unpaired t test는 자유도는 2 군의 자유도를 더한 ( n 1 -1) + ( n 2 -1)였다. 즉 자유도 ( n 1 + n 2 -2)의 t 분포를 사용한다. 그러나 Welch 검정에서는 자유도가 다르다. 자유도의 계산식은 다음과 같은 복잡한 수식이다.
자동 사유 도 =(u12n1+u22n2)2(u12n1)2n1- 1+(u22n2)2n2- 1
자유도에 대해서는 이미 설명했다 * 7 . 그러나이 공식이 어떻게 유도되었는지, 또한 왜 자유도 t 분포를 이용하면 적정하게 검정 할 수 있을까는 원 보를 읽어도 이해하지 못하고, 필자의 능력을 초과 ( 4) . 자유도는 정수가되지 않기 때문에 반올림하여 정수로하여 그 자유도의 t 분포를 사용하게된다. 통계 소프트웨어는 자동으로 계산 해주고 그 t 분포에 적용시켜 준다. 그 절차는 unpaired t test와 마찬가지로 시험한다 ( 그림 27 ).
unpaired과 paired t test는 어떻게 다른가? (그림 37)

그림 37 ■ unpaired과 paired t test의 차이
지금까지는 해당없는 독립 2 군의 차이 검정 (unpaired t test)를 언급했지만, 대응되는 관련 2 군의 차이 검정 (paired t test) 도있다. 알기 쉬운 예를 그림 37 에 기재 하였다. 2 군 별도의 쥐에서 시험하면 쥐는 지원하지 않기 때문에 지원이없는 독립 2 군의 검정이다. 한편, 같은 쥐에 투여 전과 투여 후의 비교를하는 경우 해당 있으므로 paired t test된다. paired t test의 개념은 지금까지 말해 온 unpaired t test를 이해하고 있으면 쉽게 이해할 수있다.
쉽게 쓰는 경우 paired t test의 경우에는 같은 쥐에서의 데이터이므로 투여 후 데이터 x 1 과 투여 전에 데이터 x 2 를 개별 쥐에서 비교할 수있다. 그래서 만일 6 마리의 쥐가있는로 각각의 쥐에서 차이 d = x 1 - x 2 를 계산한다. 투여 전과 투여 후 큰 변화가 있어야 d 는 제로의 전후에 분포하게 어떤 영향이 있으면, d 는 처음부터 떠난다. 파라 메트릭 시험이기 때문에 원래의 모집단은 정규 분포라고 가정하고 차이 d 역시 정규 분포하는 것으로 알려져있다. 그래서 6 마리의 d 평균 (표본 평균) d̄ 과 불편 표준 편차를 계산한다. 그런 다음 d̄ 를 표준 정규 분포를 표준화하고 공정한 표준 편차로 대체하여 t 분포에 적용은 unpaired t test와 동일하다. 자세한 내용은 졸저를 참조하라 ( 5) .
지원되는 관련 2 군의 실험은 같은 쥐에서 비교하는 것이 타당하므로 개체 차이가 사라진다 때문에 전혀 다른 쥐에 비교하는 대응이없는 독립 2 군의 실험보다 실험 계획에 따라 안정적인 데이터 를 얻을 수있는 가능성이있다 * 13 ). . 특히 개체 차이가 큰 것으로 예상되는 실험의 경우는 위력을 발휘한다. 문제없는 실험 계획을 세울 수 있다면, paired t test로 검정 할 수있는 계획하면 좋지만, 그렇지도 없다 실험은 많은 * 14 .
또한 통계 검정을 paired t test로 실시 할 곳을 unpaired로하면 모처럼의 유의 한 차이를 간과하게 될 수도 있으므로 틀리지 않도록해야한다.
비모수 검정 (그림 38)
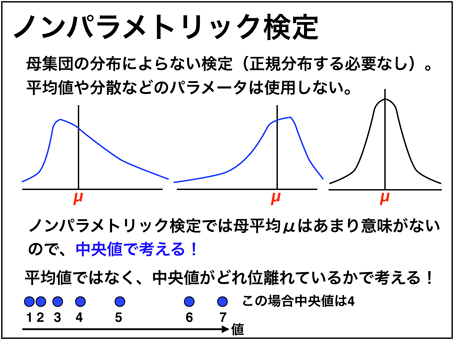
그림 38 ■ 비모수 검정
파라 메트릭 검정은 모집단의 데이터가 정규 분포하고있는 것을 전제로 조립되어있는 것은 이미 언급 해왔다. 비모수 검정은 모집단의 분포는 정규 분포 할 필요가없고, 평균과 분산 등의 매개 변수는 사용하지 않는다. 비모수 검정은 기본적으로 평균이 아닌 중앙값 생각 ( 그림 38 ). 표본의 크기 n 이 큰 경우 정규성 검정 을 통해 정규 분포로 판정되지 않은 경우에 사용할 수있다 (정규 분포로 판정 된 경우에도 사용할 수는 있지만). 또한 이상치 * 15 가있는 경우에도 사용할 수있다. 마지막 그림 7에서 언급했지만, n 이 작은 경우 모집단이 정규 분포 여부는判然としない위한 파라 메트릭 테스트에 집착 할 필요는 없다. 비모수 검정은 응용 범위가 넓다. 따라서 필자는 괴로운 데이터가 얻어진 경우에 파라 메트릭 테스트와 논빠라 메트 릭 검정을 병용하여 결과를 생각하고있다.
2 군간의 비모수 검정 (그림 39)

그림 39 ■ 2 군의 비모수 검정의 흐름
비모수 검정에서도 두 군간 및 3 군 이상의 검정법이 존재한다. 그림 39 은 두 군간의 검정법을 짚고있다. 파라 메트릭 검정 마찬가지로 해당없는 경우에 해당되는 경우 검정법이있다. 또한, 자주 사용하는 것은 우이루코쿠손의 순위 합 검정과 맨 - 휘트니 u 검정이지만, 2 군은 등분 산을 가정 하고있다 ( 그림 39 왼쪽 그래프). 그러나 n 이 적은 등 분산 여부는 판단하기 어렵다. 그래서 등분 산을 가정하지 않고, 등등 분산도 분산이 아니라도 이용할 수있다 Brunner-Munzel 검정 * 16 가 ( 그림 39 왼쪽, 오른쪽 그래프). 또한 우이루코쿠손의 순위 합 검정과 맨 - 휘트니 u 검정은 동일한 검정 결과가된다.
우이루코쿠손의 순위 합 검정의 개념 (1) (그림 40)

그림 40 ■ 우이루코쿠손의 순위 합 검정의 개념 (1)
평균도 분산도없이 어떻게 검정하는 것일까? 비모수 검정 몇 가지 있지만, 연구자는 그들 모두를 파악할 필요가 없다고 필자는 생각한다. 연구원은 비모수 검정이 어떤 원리로 검정하고 있는지를 최소한 알아두면 통계 검정에 이용한 것이 유리 여부를 판단 할 수있다. 본 세미나에서는 자주 사용되는 우이루코쿠손의 순위 합 검정 에 따라 설명한다. 이 시험 법은 파라 메트릭 검정 unpaired t test에 해당하는 ( 그림 40 ).
순위 합 검정의 기본 데이터 정렬이다. 그림 40 의 ①을 보았 으면 좋겠다. A 군과 B 군에 각각 6 개의 데이터가 해당 데이터를 작은 값에서 큰 값 (왼쪽에서 오른쪽)쪽으로 순서대로 정렬하는 (데이터의 위치를 속이 빈과 파란색 동그라미로 나타내고있다. 데이터와 데이터의 간격이 클수록 차이가 크다는 것을 나타낸다. 양 군 모두 값이 커진다 (오른쪽으로 이동) 정도 데이터가 크게 떨어져 있기 때문에, 그림 39 왼쪽 하단에있는 같은 정규 분포가 아닌 분포 것 같다. 그래서 A 군, B 군 모두 함께하여 작은 쪽부터 순서대로 우선 순위를 매기 (큰에서 우선 순위를 매기 수있다). 그렇다면 1에서 12 번까지의 번호가 붙는다.
순위 합 검정은이 순위의 숫자를 이용하여 검정 한다. 따라서 데이터의 수치는 순위하므로 평균도 분산도 관계 없어 알 수있다. 예를 들어, 12 번 데이터가 아무리 올바른 방향으로 동떨어진 큰 값도 12 번은 12 번이다. 다음으로, 도 40 의 ②를 보았 으면 좋겠다. ①에 비해 데이터의 편차가 매우 작은 2 군의 데이터이다. 이 경우도 ①과 같이 우선 순위를 매기는 ①과 ②는 동일 순위가되는 것을 알 수있다. ①과 ②의 12 개의 데이터를 순위대로 나열한 것이 ③이다. 이와 같이, 비모수 검정에서는 데이터의 편차는 관계 없으며 일정한 간격으로 늘어선 그리고 국외자가 보이지 않을 것이 특징이다 ( 그림 40 왼쪽 하단). 이러한 데이터는 "개정 증보판 : 1"에서 언급 한 순위 데이터 에 해당하며 ( 「모집단 및 표본 데이터 유형 "참조) 중간 에서 데이터를 처리하게된다. A 군은 1, 2, 3, 4, 5, 8 데이터이기 때문에, 중앙값은 3과 4 사이되므로, 양자를 더해 2로 나누어 3.5이된다 (데이터 수가 짝수 그래서 사이에있다가 홀수이면 중간 값을 취한다). B 군은 6, 7, 9, 10, 11, 12이기 때문에, 중앙값은 9.5이된다. 이 3.5와 9.5가 어느 정도 떨어져 있는지를 생각한다. 구체적인 계산에서는 A 군 (속이 빈)의 순위 합계 23이 얻어진다. B 군 (파란색 원)의 순위를 합하면 55를 얻을 수있다 ( 그림 40 ③). 순위를 합계하고 있기 때문에 순위 화라고 부른다. 이 숫자가 과연 차이가있는 숫자를 확인하게된다.
우이루코쿠손의 순위 합 검정의 생각 (2) (그림 41, 42)

그림 41 ■ 우이루코쿠손의 순위 합 검정의 생각 (2)

그림 42 ■ 순위 합 검정의 생각 (3)
지금까지 웬지 모르게 알 수는 2 군 사이에 큰 차이가 있으면 순위의 합계의 차이도 크게 될 것이라는 점이다. 만약 차이가별로없는 경우 그림 41 과 같이 속이 빈과 파란색 원형이 비교적 교대로 줄 서게된다. 이 예제에서는 파란색 원형의 중앙값은 7에서 시로 마루의 중앙값은 6이며, 그다지 차이가 없다. 순위의 합계는 블루 40 화이트 38와 가까운 값이다. 따라서 순위의 합계의 차이가 크다고 상당한 차이가있는 차이가 작 으면 큰 차이가 없다고 판단하면된다. 후에는 어떤 기준으로 판정 할 것인지를 결정하면된다.
그래서 순위 화의 조합이 얼마나 있는지를 생각한다. 우선 순위 화의 최소값은 예를 들어 화이트가 1-6이고 총 21 파란색은 자동으로 결정 7-12되어, 총 57 최대 값이된다 ( 그림 42 위). 이 조합은 1 가지 밖에 없다. 여기에서 흰색이 정해지면, 파랑은 자동으로 결정되므로, 흰색만을 생각한다. 그래서 다음에, 흰색 6 7 바뀐하면 1, 2, 3, 4, 5, 7로 총 22이며,이 조합도 1 가지 밖에 없다. 다음으로, 흰색이 1, 2, 3, 4, 5, 8된다고 총 23이지만 합계가 23이되는 조합은 1, 2, 3, 4, 6, 7 수도있다. 따라서 두 가지 있게된다 ( 그림 42 위). 이러한 관점에서 합계가 24, 25 ...되는 조합이 무엇 같습니다 있는지를 최대 57까지 계산한다. 각각의 합계에 대해 조합이 여러 가지인지 막대하면 그림 42 왼쪽과 같은 그래프를 얻을 수있다 (이 그래프는 개략적 인 그림으로 정확하지 않습니다). 그런 다음 모든 조합이 무엇 같습니다인지 합계 (여기에서는 총 X 같다). 그래서 그림 40 의 ③에서 보여준 예이다 순위 합계 23이 그래프의 어디에 있는지를 생각한다. X대로 전체를 100으로 순위 합계 23의 2 가지가 예를 들어, 양쪽의 2.5 % 이내에 들어 오면 상당한 차이가 있다고 판정 (유의 수준 5 %, 양측 검정의 경우) ( 그림 42왼쪽 그래프). 이 판정은 파란색 경우의 순위 합계 55에서 생각해도 그래프에서의 위치는 좌우 반대측되지만, 동일한 결과를 얻을 수있다 ( 그림 42 왼쪽 그래프). 파라 메트릭 테스트에서 설명 했으므로 자세한 내용은 언급하지 않지만, 대립 가설로 A> B가 가정 있다면 단측 수도있다. 이 순위 합 검정에서 유의 한 차이를 구하는 원리이다 * 17 .
또한, 상술의 순위 합 검정의 예는 해당이없는 독립 2 군의 검정이다 우이루코쿠손의 순위 합 검정 이며, t 검정은 unpaired t test에 해당한다. 비모수 검정에서도 해당되는 관련 2 군의 검정 (paired t test에 해당)이있다. 대표적인 것으로는 그림 39 오른쪽으로 기재했다. 우이루코쿠손의 순위 합 검정에 대해서는 우이루코쿠손 부호있는 순위 검정 이있다. 여기에서는 자세히 설명하지 않지만, "대응되는"기본 개념은 파라 메트릭의 paired t test와 같으며 해당 데이터 x 1 과 x 2 의 차이 d를 순위로 대체 생각된다. 자세한 내용은 졸저 ( 5) 또는 "금방 알 통계 분석」( 6) 을 참조하기 바란다. 유사한 명칭이기 때문에 틀리지이다. 또한, 통계 응용 프로그램에서는 "우이루코쿠손 순위 검정」라는 명칭으로 해당 탓인지 응대에 체크하는 등 절차가있다. 이것은 위의 두 검정법에 대응한다.
비모수 검정의 장점, 단점 (그림 43)

그림 43 ■ 비모수 검정의 장점, 단점
비모수 검정의 원리를 알게되면 훨씬 더 크게 바라つい데이터에서도 그렇지 않아도 검정 결과가 동일 것에 대해 그렇게 좋은 것일까라고 생각하지 않을까? 나도 처음에는 그랬다. 그림 43 에 장점, 단점을 보여주고있다. 모집단이 정규 분포하는 경우는 검출력이 떨어지는 것 같지만, 그리 크지 떨어지는 것은 아니다 ( 2) . 또한 이상치 가있을 때, 기각 검정 으로 분리 할 가능하게되는 경우도 있지만, 안이 분리 할에 문제가 있으므로 분리하지 않고 비모수 검정을 실시하고 가치가있다. 비모수 검정에서 유의 차가 얻지 못하면 포기 수있다. 국외자 취급에 대해서는 다음에 언급하지만, 고민 데이터가있을 때는, 우선 파라 메트릭 검정과 비모수 검정, 또 기각 검정 결과를보고 나서 생각은 어떻게 일까?
또한, 비모수 검정은 표본의 크기 n 이 작 으면 파라 메트릭 시험보다 시험이 어려워진다. t 검정은 두 군 모두 n = 3에서 검정있다. 그러나 유의 수준 5 %에서 양측 검정의 경우 우이루코쿠손의 순위 합 검정은 필요한 최소 n 은 2 군 모두 4이다. 이 경우 그림 42 위에서 두 번째 줄처럼 속이 빈과 파란색 동그라미가 완전히 분리되어있는 경우에만 의미가되기 때문에 매우 어렵다. 또한 우이루코쿠손의 부호있는 순위 검정의 경우 양측 검정에서 가장 필요한 n 은 6이다. 따라서 이러한 검정은 필요한 최소 n 의 검정은 가혹하기 때문에 그보다 약간 많은 n 이상으로하는 것이 무난하다.
결론
다음 최종회는 3 군 이상의 경우 검정이며, 일원 분산 분석 , 다중 비교 , 이원 분산 분석 을 중심으로 기술한다. 연구 논문이나 학회 발표에서 3 군 이상 시험에서 다중 비교를 이용하지 않고 부적절하게 2 군의 검정법, 예를 들어 t 검정을 반복하는 예는 감소하고 있지만, 아직 완전히 없어져 않은 . 왜 t 검정에서는 안되는 것인지를 이해해야한다. 또한 이원 분산 분석시 군간 비교는 실수하지 검정법에서 이루어지고있는 것이 적은 듯 크게 혼란하고 있기 때문에 올바른 이해가 필요하다.
Reference
1 ) 이치하라 키요시 : "바이오 사이언스의 통계학",南江堂1990.
2 ) 아다치 켄이치 : "편안 생물 통계학", 중산 서점, 1998.
3 ) http://www2.vmas.kitasato-u.ac.jp/lecture0/statistics/stat_info03.pdf
4 ) BL Welch : Biometrika , 29 , 350 ( 1938 ).
5 ) 이케다郁男: "실험에 사용 곳뿐만 생물 통계 2 김기홍 홍 개정판"羊土社2017.
6 ) 석촌 사다오 : "금방 알 통계 분석", 도쿄 서적, 1993.
* 1 * 1 이것은 매우 중요한 포인트로, 중심 극한 정리 라고 불린다. 표본의 크기 n 이 클수록 표본 평균 X̄ i 의 평균은 모평균 μ에 접근하고 그 분산은 모집단 분산 σ 2 의 1 / n 에 접근한다. n 이 클수록σ/n--√은 작아 지므로 모평균의 범위가 좁혀 오는 것을 의미한다 ( 그림 17 아래 그래프). 또한, n 이 큰 경우 모집단이 정규 분포뿐만 아니라 정규 분포에서 벗어나 있어도 그 모집단에서 채취 한 표본 평균의 분포는 정규 분포한다는 재미있는 성질이있다.
* 2 실험 동물의 모집단을 예로 든다면, 예를 들어 그 중에서 6 마리를 표본으로 추출하여 측정 한 매개 변수의 표본 평균을 계산한다. 이 작업을 반복하여 얻어지는 많은 표본 평균의 편차는 각각 벗어난 데이터가 있어도 평균화되기 때문에 모집단의 데이터의 편차보다 작을 수는 예상 할 수있다이다 왁스.
* 3 이전에도 말했지만, 본 세미나의 모든 그림은 필자가 개략적으로 작성된 것이며 정확한 것은 아니다.
* 4 이 식은 왜 표준 정규 분포의 값으로 변환되는지 궁금해 수도 있지만, 수학적 증명은 이루어지고있다.
* 5 * 5 개 총설에서는 불편 분산 u 2 를 루트 값 u를 불편 표준 편차와 이름, 어머니 표준 편차를 추정하는 값으로 논하고있다. 그러나 u는 참 불편 표준 편차가 아니다 ( "개정 증보판 : I '의 * 13 참조). 정확한 불편 표준 편차는 차이가 있으며, 특히 n 이 10 이하로 작을수록 차이가 크다.
* 6 * 6 이 점이 u는 "편견"이 아님을 보여주고있다. "편견"이란 치우 치지 않음으로써 편견없이 모집단을 추정 할 수 있음을 의미한다. 만약 u가 "공정한"이면 모집단 표준 편차 σ를 추정하는 값이되므로, σ를 u로 대체해도 정규 분포가되는 것이다. 그런데 u는 σ는 차이가 있기 때문에 정규 분포와는 조금 어긋난 t 분포된다. n 이 작을수록 차이가 커지기 때문에 t 분포는 정규 분포와 크게 차이, n 이 클수록 정규 분포에 가까운 분포가된다 ( 그림 21 의 그래프 참조).
* 7 * 7 t 분포는 실제로 n 대신 자유도 n -1에 따라 모양이 변한다. 자유도는 여러 번 등장했다. 불편 분산의 계산은 제곱의 합을 n 으로 나누는 것이 아니라, 자유도 n -1로 나누면 모집단 분산을 추정 할 수있는 값 이 될 것이라고 말했다. 앞으로는 n -1 이외의 자유도도 등장하지만, 어떤 경우에도 자유도를 이용하여 모집단의 정보를 추정 할 수있다 라고 생각하면된다. "바이오 사이언스의 통계학"는 자유도는 데이터의 편차와 편차를 예측 할 때 (즉, 분산과 표준 편차를 계산할 때) 다른 사람과 독립적으로 취급 할 데이터 수 의 수라고 있다 ( 1) . 매우 이해하기 어렵지만, 예를 들어, 모집단에서 표본을 6 개 채취 한 경우 각각 무관 한 독립적 인 표본 경우 자유도는 6이다. 그러나 이미 언급했던 것처럼 불편 분산을 계산할 때, 계산에 표본 평균이 들어있다. 식 표본 평균이 있으면, n 이 6의 경우 5 개의 데이터가 있으면 6 개째의 데이터는 표본 평균 × 6 (5 개의 표본 데이터의 합계)을 차감하면 구해진다. 즉, 독립적으로 취급 할 데이터 수는 5이며, 6 번째는 자동으로 정해 버렸 자유롭게 움직일 수 없다. 따라서 자유도는 1 줄어 5가된다. 즉, 표본의 크기를 n 하면 자유도는n -1이되는 것이다.
* 8 또한, 학회 발표에서 슬라이드 표본의 크기 n 과 표본 평균 ± SE인지 ± SD인지 표기하지 않은 발표가 많이 보인다. 이러한 중요한 정보이며, 그 표기는 연구자로서의 기본이다. 쓰고 잊어 끝나는 것은 아니다.
* 9 이 5 % (0.05)을 결정한 것은 통계적으로 유명한 Ronald Fisher 것으로 알려져있다. 사실 0.05에 과학적 근거는없는 것이다. Fisher가 0.07로 결정하면 그렇게 정해진지도 모른다.
* 10 첫째 종의 과오 에 대해 차이가있는 대립 가설을 기각하여 차이가 없다고 해 버리는 실수를 두 번째 종의 과오 라고 부른다. 이들은 통계 서에 자주 등장하고 이해하기 어려운 단어이다.
F 분포는 자유도에 따라 모양이 변화한다. 여기에서는 2 군이기 때문에, 제 1 군 눈을 분자로하고, 2 군 눈을 분모하면 자유도 n 1 -1과 n 2 -1의 F 분포된다. 또한, 그림 34 의 F 분포의 그림은 필자가 적당히 그린 것으로 정확한 그림이 아니다.
* 12 t 검정에서도 언급 한 바와 같이 동일한 모집단에서 생각해 봤는데 때문에 분산이 아니라고 단정 할 수없는 것은 이해해 주실 것이다.
* 13 같은 쥐에서 이전과 이후의 데이터이므로 분산은 같은 생각 등 산성 검정은하지 ( 그림 35 ).
* 14 인간은 개체의 편차가 크기 때문에 해당이없는 독립 2 군 시험은 표본의 크기를 매우 크게 할 필요가있다. 그러나 피험자를 모으는 것은 대단하다. 그래서 해당되는 관련 2 군의 시험을 이용하는 사례는 많다. 예를 들어, 시험 전후의 혈압을 비교하는 등 시험이다. 한편, 장기 시험을 내면 여름과 겨울에 혈압이 변동하는 등 계절의 변화 등의 문제가 생긴다는 단점이 목적을 잘 생각해서 실시 할 필요가있다.
* 15 다른 값을 크게 벗어나는 값이다. 연구에서는 자주 뵙겠 어떻게 처리할지 고민하는 경우가 많다. 통계 검정에있어서 국외자 취급에 대해서는 다음에 기술한다.
* 16 필자는이 시험 법의 원리 등의 지식이 없기 때문에 소개에 멈춘다.
* 17 우리는 논문 등에 데이터를 표시하는 경우, 표본 평균 ± 표준 오차 (SE) 또는 표준 편차 (SD)를 쓴다. 이들은 파라 메트릭 테스트를위한 파라미터이며, 비모수 검정을 실시한 경우이를 표기하는 것은 의미가 없다. 그러나 논문이나 학회 발표에서는 관습 적으로 이러한 표기가 이루어지고있는 경우가 대부분이다. 생각해 보면 이상하다.
This page was created on 2019-07-09T17 : 30 : 06.482 + 09 : 00
This page was last modified on 2019-08-16T11 : 48 : 51.000 + 09 : 00
'논문을 위한 통계' 카테고리의 다른 글
| 통계 검정을 이해하지 않고 사용하는 사람들을 위해 III이케다 郁男 (0) | 2021.04.16 |
|---|---|
| 개정 증보판 : 통계 검정을 이해하지 않고 사용하는 사람을 위해 I (0) | 2021.04.16 |
| 표 예쁘게 그리기 (0) | 2020.03.02 |
| 통계 사이트 모음 (0) | 2020.02.18 |